Study Population & Sampling
Table of Contents

Clearly defining your study population and sampling method is a vital step in research. It precisely identifies who or what you’ll study and justifies your choices.
Purpose: In your research plan, you must clearly state your study population and explain why it’s the most appropriate group for your research question. This section justifies your selection to the reader.
DEFINITIONS:
Sample: A sample is a smaller, manageable subset taken from a larger population. Researchers use samples because studying entire populations is often impossible due to limited resources like time and money.
Study Sample: This is the actual group of individuals or units from your accessible population who participate in your study. You collect data directly from the study sample.
Sampling: Sampling is the process of carefully selecting a sample from a population. The goal is for this smaller sample to accurately represent the larger population, so findings from the sample can be generalized back to the whole group. Sampling becomes essential when populations are large.
Sample Size: Sample size is simply the number of participants included in your study sample. For example, a study might aim for a “sample size of 150 people.” Larger samples generally increase accuracy, but practical constraints exist.
Population: Population refers to the entire collection of individuals, items, or cases that share specific characteristics relevant to your research question. It’s everyone (or everything) you could potentially study.
Target Population: The target population is the ideal population you want to learn about and to which you hope to apply your research findings. It’s the broadest group of interest (e.g., “all teenagers with asthma globally”).
Accessible Population: The accessible population is the more realistic subset of the target population that you can actually reach and recruit for your study, given practical limitations. It’s a narrowed-down, feasible group (e.g., “teenagers with asthma living in clinics within a specific city this year”).
Homogeneous Population: A homogeneous population is very uniform; its members are highly similar in the characteristics relevant to your study. This can sometimes allow for smaller sample sizes.
Heterogeneous Population: A heterogeneous population is diverse; its members differ significantly in key characteristics (like age, gender, etc.). Heterogeneous populations often require larger, more representative samples.
Sample Study vs. Census Study:
Sample Study: Studies a sample to infer information about the larger population. This is the most common approach.
Census Study: Studies every single member of the population. Only feasible for very small populations.
Why Sample? (Importance)
Sampling is essential for making research practical and effective:
Manage Large Populations: Makes studying very large or geographically spread-out groups feasible and manageable.
Reduce Costs: Significantly lowers research expenses compared to studying everyone.
Save Time: Speeds up data collection and analysis considerably.
Improve Potential Accuracy: With focused effort on a smaller sample, data quality can sometimes be higher, leading to potentially more accurate findings than a rushed census.
Simpler Logistics: Makes the research project easier to organize and execute.
Limit Destructive Impact: Crucial when research involves damaging or using up the items being studied (e.g., in product testing or some medical tests).
Standard in Medical Research: Ethically and practically necessary in most medical studies involving patients.
Methods of Sampling / Sampling Methods
Sampling methods are procedures researchers use to select sample members from a population. There are two main categories:
Random (Probability) Sampling Methods
Non-random (Non-probability) Sampling Methods
The best sampling method depends on several factors, including:
Population Type: The characteristics of the population you’re sampling from.
Desired Accuracy: The level of precision you need in your results.
Resource Availability: Time, budget, and personnel constraints.
Population Homogeneity: How similar or diverse the population is.
Urgency of Findings: How quickly results are needed.
Random Sampling Method
In random sampling, every member of the population has an equal chance of being selected for the sample. This is based on probability.
Advantages of Random Methods:
Equal Opportunity: Each population member has the same chance of selection, promoting fairness.
Bias Reduction: Helps to minimize or eliminate researcher selection bias.
Enhanced Validity: Improves the likelihood that the sample accurately represents the population, strengthening study validity.
Ease of Administration: Can be relatively straightforward to implement, depending on the specific type.
Statistical Analysis: Allows for the use of statistical methods to analyze data and generalize findings.
Disadvantages of Random Methods:
Sample Frame Required: Often necessitates a complete sample frame, a list of all population members, which may not always be available.
Potential for Disproportionate Strata Representation: In diverse populations, there’s a chance that subgroups (strata) might be under- or over-represented in the sample by chance, even if random selection is used.
Random Sampling Methods Include:
Simple Random Sampling
Stratified Random Sampling
Systematic Sampling
Multistage Sampling
Territorial Sampling
Cluster Sampling
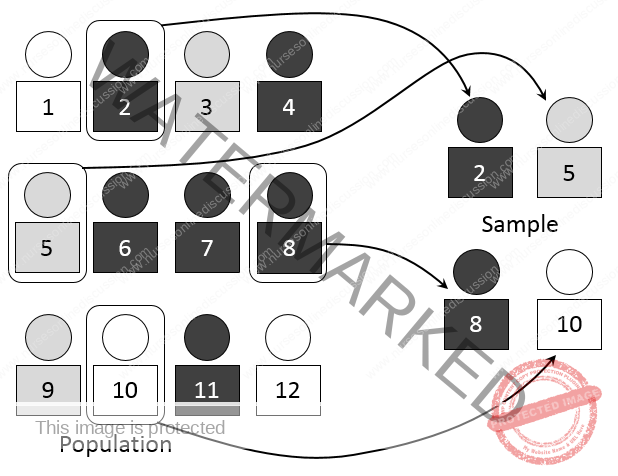
Simple Random Sampling
The core idea of simple random sampling is that each item or individual in the population has an equal chance of being selected for the sample. This selection is purely based on chance.
One method to achieve simple random sampling is using the lottery method.
Lottery Method Procedure:
Assign Identifiers: Each member of the population is given a unique identifier, such as a number or name.
Prepare Tickets: These identifiers are written on identical pieces of paper.
Mix Thoroughly: The paper tickets are folded to conceal the identifiers, placed in a container (like a bowl), and mixed completely.
Blind Selection: A researcher, often blindfolded to ensure impartiality, draws tickets one by one from the container without replacement (meaning a selected ticket is not put back in).
Sample Formation: This process continues until the desired sample size is reached. The individuals corresponding to the drawn tickets form the simple random sample.
Summary of Simple Random Sampling Technique:
Define Population: Clearly identify the population of interest by specifying relevant characteristics.
Determine Sample Size: Decide on the required sample size for your study.
Create Sample Frame: Develop a sample frame, which is a complete list of all individuals or items within your defined population.
Random Selection: Select the sample members randomly from the sample frame. This can be done using the lottery method described above or with a random number table (a table of randomly generated digits).
Advantages of Simple Random Sampling: (Mirrors advantages of general random sampling)
Provides equal selection probability for all population members.
Minimizes selection bias.
Enhances study validity by promoting representativeness.
Relatively easy to implement.
Disadvantages of Simple Random Sampling:
In populations with distinct subgroups (heterogeneous populations), there is a possibility that a simple random sample might, by chance, under-represent or over-represent certain subgroups. This can introduce bias if these subgroups are important for the research question.
Stratified Random Sampling
In stratified random sampling, the population is divided into distinct subgroups, known as strata, before sample selection occurs. Researchers use this method when they want to ensure specific subgroups are adequately represented in the sample.
Purpose of Stratification: To guarantee representation of key subgroups (strata) within the sample, reflecting their proportions in the overall population. For instance, a researcher might want to ensure both males and females are included in the sample in proportions mirroring the population.
Maintaining Proportionality: Crucially, the percentage of each subgroup in the sample should mirror its percentage in the overall population. For example, if a population is composed of 70% Group A and 30% Group B, the sample should also ideally reflect this 70/30 split.
Addressing Simple Random Sampling Limitations: Stratified random sampling is employed to overcome a potential weakness of simple random sampling, where, by chance, certain subgroups in a diverse population might be under- or over-represented in the sample.
Stratified Random Sampling Technique Steps:
Determine Sample Size: Decide on the total sample size needed for the study.
Define Strata: Establish strata (subgroups) based on relevant criteria. These criteria should be meaningful for the research question (e.g., age groups, socioeconomic status, ethnicity, gender).
Allocate Sample Proportionally: Determine the number of participants to select from each stratum. This is done proportionally, ensuring each stratum’s representation in the sample matches its proportion in the population.
Random Selection within Strata: Use random sampling techniques (like simple random sampling or systematic sampling) to select the required number of participants within each individual stratum.
Example:
Imagine a school population of 1000 students, with 600 boys (60%) and 400 girls (40%). A researcher aims to draw a sample of 100 students.
Population Proportions:
Boys: (600 / 1000) * 100% = 60%
Girls: (400 / 1000) * 100% = 40%
Sample Allocation: The sample of 100 must proportionally reflect these percentages:
Boys in Sample: 60% of 100 = 60 boys
Girls in Sample: 40% of 100 = 40 girls
Random Sampling within Strata: The researcher would then:
Randomly select 60 boys from the list (stratum) of all boys in the school.
Randomly select 40 girls from the list (stratum) of all girls in the school.
This process ensures the final sample of 100 students accurately reflects the gender distribution within the entire school population through stratified random sampling.

Systematic Sampling
In systematic sampling, the population is organized based on a specific sequence or order. Sample members are then selected at consistent intervals from this ordered list. Crucially, to minimize bias, the very first selection (starting point) must be chosen randomly.
To determine the selection interval: divide the total population size by the desired sample size. This interval then dictates how often you select a member from the ordered list.
Example:
Imagine you need a sample of 8 houses (sample size) from a street containing 120 houses (population).
Calculate Interval: 120 houses / 8 houses = 15 (This is your selection interval). You will select every 15th house.
Random Start: Choose a random starting point between 1 and 15. Let’s say you randomly select 7.
Systematic Selection: Starting with house number 7, select every 15th house thereafter. The selected houses would be: 7, 22, 37, 52, 67, 82, 97, and 112.
Important Note: Systematic sampling is not considered purely random. While the starting point is random, once that’s set, the subsequent selections are predetermined by the interval. For instance, in the house example, houses 1-15 have a chance of being the starting point and thus selected earlier in the sequence, while houses 16-120 cannot be the first house chosen.
Systematic sampling is most effective for large, relatively uniform (homogeneous) populations and is often simpler to carry out than simple random sampling.
Summary of the Systematic Sampling Process:
Define Population: Clearly identify the population you are studying.
Order Sample Frame: Create a list of all population members, arranged in a specific order (e.g., alphabetical, numerical).
Determine Interval: Calculate the sampling interval by dividing the population size by the desired sample size.
Systematic Selection with Random Start: Begin at a randomly chosen point on your ordered list, and then select every nth member (where n is your calculated interval) to form your sample.
Cluster Sampling
Cluster sampling is a method where the population is first divided into groups called clusters. Then, instead of selecting individuals directly, the researcher randomly selects one or more clusters from the entire set of clusters. Once clusters are chosen, all individuals or units within the selected clusters become part of the sample.
Key Points:
Clusters are Randomly Selected: The random selection happens at the cluster level, not the individual level.
Entire Cluster Included: Once a cluster is chosen, every member within that cluster is included in the sample.
No Individual Listing Needed (Sometimes): Cluster sampling is particularly useful when creating a complete list of individuals across a large geographical area is impractical or impossible. Instead of listing individuals, you can use a map showing area subdivisions (political, geographical, etc.) for cluster selection – this is sometimes called area sampling.
In essence: Randomly choose groups, then study everyone in those chosen groups.
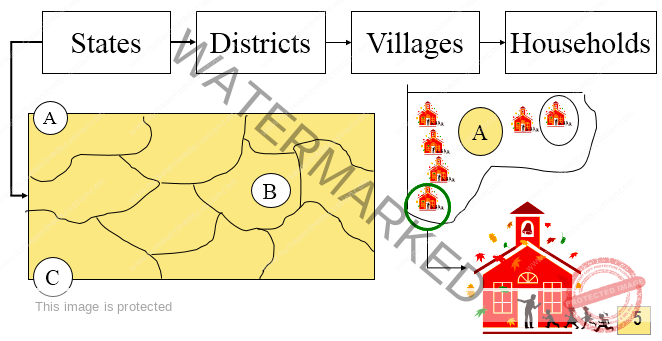
Multistage Sampling (Multistage Cluster Sampling)
Multistage sampling, also known as multistage cluster sampling, is an extension of cluster sampling designed to be more efficient and cost-effective, especially when dealing with large, geographically dispersed populations.
Addressing Cluster Sampling Limitations: While cluster sampling selects entire clusters, multistage sampling acknowledges that studying everyone in all selected clusters can still be too resource-intensive or unnecessary for the research objectives.
Hierarchical Cluster Selection: Multistage sampling involves multiple levels or stages of cluster selection in a hierarchical manner. Instead of using all members of the initially chosen clusters, researchers take it a step further by randomly selecting a sample of individuals within each chosen cluster.
Example: Household Survey in a Metropolitan Region
Stage 1: Districts (Primary Clusters): Divide the entire metropolitan region into geographical districts. Randomly select a sample of districts from all districts in the region.
Stage 2: Blocks (Secondary Clusters): Within each of the districts selected in Stage 1, further divide them into smaller geographical blocks. Randomly select a sample of blocks from within each selected district.
Stage 3: Dwellings (Final Sampling Units): Within each of the blocks selected in Stage 2, create a list of all dwellings (households, apartments). Randomly select a sample of dwellings from within each selected block.
Outcome: In this three-stage example, the final sample consists of individuals residing in the dwellings selected in the final stage.
Key Advantage: Multistage sampling avoids the need to create a complete list of every dwelling (or individual) in the entire metropolitan region at the outset. Listing is only required for the selected blocks at the final stage, significantly reducing the effort and resources needed for large-scale surveys.
Non-Random Sampling Methods
Non-random sampling methods are characterized by the fact that:
Unequal Selection Chance: Some members of the population have no chance of being selected for the sample.
Unknown Probability: For those who could be selected, the probability of selection cannot be accurately determined. Selection is not based on chance but on other criteria.
Qualitative Research Focus: These methods are primarily used in qualitative research, where the goal is often in-depth understanding rather than statistical generalization to a population.
Advantages of Non-Random Sampling Methods:
Cost-Effective: Generally less expensive to implement than random sampling.
Simpler Implementation: Often have a less complex approach to sample selection.
Faster Results: Can yield quicker results compared to probability sampling, as recruitment may be faster.
No Sample Frame Needed (Often): May not require a complete list of the entire population, making them practical when such lists are unavailable.
Disadvantages of Non-Random Sampling Methods:
Bias Susceptibility: Prone to human error and bias because selection is not randomized and relies on researcher judgment or convenience.
Limited Generalizability: Findings are generally not appropriate for generalizing beyond the specific sample studied to the broader population. Conclusions are specific to the sample itself.
Inappropriate for Statistical Inference: Statistical analysis designed to generalize to a population (e.g., confidence intervals, hypothesis testing) is not valid when using non-random sampling methods because the sample may not be representative.
Types of Non-Random Sampling Methods:
Convenience Sampling:
Selection Basis: Sample selection is based on the researcher’s convenience and accessibility. Participants are chosen because they are readily available, easy to reach, and willing to participate.
Example: Choosing study participants from the two parishes “nearest” to the researcher simply for ease of access.
Purposive/Judgmental Sampling:
Selection Basis: Sample selection relies entirely on the researcher’s judgment and specific research interests. The researcher deliberately selects participants who are believed to be particularly knowledgeable, experienced, or relevant to the study’s purpose.
Example: Choosing to interview only nurses who are currently “on duty” because they are readily available and assumed to have relevant insights.
Snowball Sampling Method:
Selection Basis: Participants are recruited through referrals. Initial participants are asked to recommend other potential participants who meet the study criteria. This method is useful for reaching populations that are hard to access directly.
Process: Each interviewed person suggests further respondents who they know can provide valuable data. The sample “snowballs” as referrals expand the participant pool.
Quota Sampling:
Analogy to Stratified Sampling: A non-probability counterpart to stratified random sampling.
Process: The population is first divided into subgroups (quotas) based on specific characteristics, similar to stratification. However, instead of random selection within each subgroup, researchers use judgment to select participants from each quota to meet a pre-set proportion. Randomness is not used in the final selection.
Accidental Sampling:
Selection Basis: Participants are included in the sample purely by chance or accident, not through any deliberate selection strategy. The sample is formed incidentally based on who happens to be available at a particular place and time.
Example: Interviewing “every student who passes by” a specific location (like a university gate) without any pre-defined selection criteria.
Important Notes on Sampling Errors:
i) Sampling Errors: These errors arise because conclusions are drawn about a whole population based on a smaller sample. Sampling errors are more likely when a sample is small and non-random. Larger, randomly selected samples generally reduce sampling error.
ii) Non-probability Sampling and Error Estimation: Non-probability sampling methods do not allow for the estimation of sampling error. Statistical methods to quantify sampling error (e.g., calculating confidence intervals) are not valid with non-random samples.
Types of Sampling Errors:
Random Error: This is a chance error that can lead to inaccurate results simply due to random variation in the sample. Random error can be reduced by increasing the sample size.
Systematic Error (Bias): This is a more serious error resulting from a flaw in the sampling method or research design itself, leading to a consistent distortion of results in a particular direction. Systematic error is due to bias, not chance. Increasing sample size alone will not fix systematic error. It requires addressing the source of the bias in the study design or sampling procedure.
Diploma in Midwifery
Get in Touch
(+256) 790 036 252
(+256) 748 324 644
Info@nursesonlinediscussion.com
Kampala ,Uganda
© 2025 Nurses online discussion. All Rights Reserved Design & Developed by Opensigma.co

